User:Wmonroe4/Vectors and Quaternions
I love vectors.
This is not a typical feeling. Most people find them either scary or completely pointless, or a combination of the two. The problem is that most people are introduced to vectors through 11th-grade pre-calculus, where their teacher shows them that there's something called a "dot product" and a "cross product", makes them do a few calculations, then moves on to limits or whatever else you do in pre-calculus. (Don't worry, I've forgotten too.)
The next place you see them, if you've gone this far in math, is Math 51, where they are mostly a notational shorthand for the solution to mind-numbing systems of linear equations, to be solved by Gaussian elimination. Gaussian elimination, if you haven't had to do it, is almost entirely arithmetic, aside from the fact that everything is stuffed into matrices. These arithmetic calculations can be done by a computer. They should be done by a computer. That is their rightful place.
This is why I was lucky to be exposed to vectors first through 3-D video game development, manipulating them by computer even before I saw them in high school. I learned about vectors by doing things with them, seeing what they mean, as opposed to what is going on with the numbers, which, frankly, does not matter in the slightest.
My hope is that working on Meru will help give you the same love for vectors that I have. The goal of this page to help you take the first step in that direction, and that first step is realizing that vectors are incredibly useful, once you no longer have to do the calculations by hand. So without further verbose introduction, I present:
How to Put Vectors and Quaternions to Good Use: A guide for game programmers
What's a vector?
It's a bunch of numbers. Or it's a thing with length and direction. These are both definitions of vector, and they're both equally valid. Since the whole point of this page is to mention the ways in which vectors are intuitive and useful, the second definition seems at first glance to be the best one to think about in day-to-day use.
There's an even more useful way to think about a vector, though: a vector is a point. This may seem strange at first. In fact, if you ask a mathematician, she'll tell you that that's just wrong, and strictly speaking, she's right—vectors and points aren't really the same. Treating them as the same thing, however, is an extremely useful practice in 3-D game programming. The most important reason is that it gives you an intuitive link between the collection of numbers and the length-and-direction "arrow" picture. Hopefully high school math has gotten you used to putting points on a Cartesian x-y plane, showing you that a point can be represented by—yes—a bunch of numbers.
But how does a point have length and direction? Well, the point isn't really the whole picture. What that bunch of numbers really tells you is the relationship between that point and some other point. That other point is the origin, some arbitrary spot that we've proclaimed to be the point represented by (0, 0, 0). The fact that we have an origin is what makes points and vectors interchangeable. Now that you have two points, just draw an arrow pointing from the origin to your point, and you've got something with length and direction. Sometimes you won't need to picture the arrow, but if you're lying awake at night wondering whether you are alone in isotropic space, it can be comforting to know that the origin is always there somewhere, throwing invisible arrows out to all your points.
What you can do with one vector
Well, you can take a look at it and examine its properties. Let's make ourselves a vector:
>>> var v = new util.Vec3(4, 2, -3);
>>> v.x
4
>>> v.y
2
>>> v.z
-3
It's clearly got a bunch of numbers. (From here on out you can assume every vector has exactly 3 numbers, unless I specifically say otherwise. A vector doesn't have to be 3-D, but we'll be working mostly with the 3-D kind, so that's what I'll be talking about.) It also has a length:
>>> v.length()
5.385164807134504
>>> v.lengthSquared()
29
lengthSquared isn't always as useful as length, but there's one major advantage to it: it's extremely fast to calculate. Finding the length proper involves taking a square root, which is a lot slower. The best use case for lengthSquared is when you are comparing two lengths: comparing the lengths-squared is faster and works just as well.
What about direction? It's kind of hard to print a direction, but you can do an okay job by coming up with a unit vector—quite simply, a vector of length 1. By arbitrarily saying that a vector must be of length 1, you're saying that you are ignoring its length and focusing only on its direction. This is how you get a normal vector in Emerson:
>>> v.normal()
{
x: 0.7427813527082074, // Emerson is printing vectors as y, z, x at the moment.
y: 0.3713906763541037, // This film edited for content and formatted to fit your screen.
z: -0.5570860145311556
}
Notice that this is in the same direction as (4, 2, -3), our original: it's a large-ish amount in the x direction, a slightly smaller amount in the y direction, and a moderate amount in the negative z direction. You can do the math, though, or just trust the computer: this new vector has length 1. "Chopping" a vector down to length 1 like this is called normalizing the vector. Right now it's not clear why this is useful, but be patient: unit vectors come in handy in a surprising number of situations.
Normalizing a vector gives you a new vector with the same direction and a different length. There's another function that does this in a more general way, letting you multiply the vector's length by an arbitrary factor. It's called scale:
>>> v.scale(3)
{
x: 12,
y: 6,
z: -9
}
See what happened? You got a vector that was triple the length of the original, again in the same direction. There's also a function div that divides everything by the number you give it. In fact, with this, you can write normal yourself: it's just
return this.div(this.length());
This is pretty much* all the actual Emerson code does.
You can also pass in zero to scale, in which case it will just give you (0, 0, 0), the null vector. You can even pass in a negative number, which in addition to changing its length, makes it point in the opposite direction. Of course, it's still just multiplying numbers behind the scenes. This is just what happens when you multiply all three components by zero or by a negative number. Finally, there's a special shortcut function for scaling by -1, that is, flipping the vector to the opposite direction without changing its length:
>>> v.neg()
{
y: -2,
x: -4,
z: 3
}
*There's also a minor edge case for when you try to normalize a vector of length zero, to avoid division by zero. That's all there is to it, though.
Adding and subtracting vectors
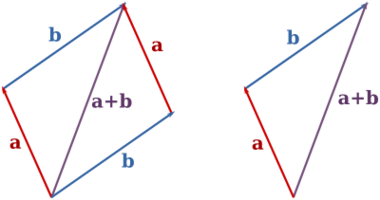
Here's where things get interesting. Pretty much all of manipulating 3-D objects is combining vectors in various ways. There are a few ways to think about vector addition. First, you can imagine sticking the tail of one arrow onto the head of the other, with the sum being a third arrow going from the remaining (non-connected) tail to the remaining head. You can also imagine this as "moving along" one vector, then from there "moving along" the other. The sum is how far, and in what direction, you moved total.
The other way to think of it is this: what point would one vector represent, if the point represented by the other were the origin? This is a particularly useful interpretation in 3-D graphics, where you can have an origin for an object (say, one of those winged frog things from Spore that we've been working with) and a vector representing a point on that object (say, the frog's left eye), which you would then add to a vector representing where the frog is in the world to get an absolute position for the left eye in terms of the whole world.
Notice how I've been careful to say "one vector" and "the other", without mentioning "a", "b", "the first", or "the second". This is because like normal addition, it doesn't matter in what order you add them. Vector addition is commutative.
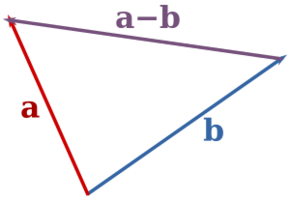
From these images you might be able to guess how subtraction works. Just add the first vector to the opposite of the second. Probably the most useful way to think about this is, "how do I get from the point represented by the second to the point represented by the first?" Notice that here the order does matter—vector subtraction is not commutative. Just like normal subtraction, vector subtraction is anticommutative. That is,
<math>\vec{a} - \vec{b} = -(\vec{b} - \vec{a})</math>
or in Emerson:
a.sub(b) /* == */ b.sub(a).neg()
Why have I commented out the ==? It turns out == doesn't work for vectors, just like it doesn't work for strings in Java. Unfortunately, there isn't an equals for vectors in Emerson. You can use this function, if you really need to do this test:
function VecEquals(a, b) { return (a.x == b.x && a.y == b.y && a.z == b.z); }In any case, these are floating point numbers, so you want to be careful about comparing them.
Here's a couple of pictures to help you understand things a bit better:
Adding two vectors. The triangle picture, I feel, is a better way to think about addition in general; the parallelogram picture is mainly helpful for showing why addition is commutative. (If you can't see the arrowheads, all of the vectors point generally upwards.)
Subtracting one vector from another. The arrowhead of the purple vector points to the left.
Products of vectors
You probably know from pre-calculus and/or Math 51 that there are two ways you can "multiply" two vectors: the dot product and the cross product. Rather than show you all the x's, y's, and z's dancing around the page, I'll just show you another pair of pictures.
The dot product
|A| is just the length of A.
So as not to give you any bad foundations, I'll say up front that the picture on the left is slightly wrong. The dot product formula, as you may remember, is not |A| cos θ but rather |A| |B| cos θ. Hence, the length in the picture is not labeled A · B: A · B is actually that length times the length of B.
The picture is correct in one important case, however, and that's when B is a unit vector. In that case, the dot product represents how much A points in the direction given by B. What if A points in the opposite direction? In that case, you'll get a negative dot product. How about if they're perpendicular? Here, they neither agree nor disagree, so the dot product is neither positive nor negative—it must be zero. The dot product of two perpendicular vectors is zero. In addition, if either vector is zero (the null vector), the dot product has to be zero: everything is perpendicular to zero.
In the general case, you can think of the dot product as measuring how much the two vectors "agree": are they going in the same direction (positive or negative?), and how far do they go (how big is the dot product?)? Double either vector, and the dot product also doubles. Double both of them, and the dot product gets multiplied by 2 · 2 = 4. It can be useful to think of projecting one vector onto the other when visualizing the dot product, but remember that neither vector is special: like normal multiplication, the dot product is commutative.
The cross product
The first thing you should see in the picture on the right is that the cross product of two vectors is a vector, perpendicular to both. The area-of-the-parallelogram description isn't a bad one, as descriptions of vector math go. A cooler way to think about it is to imagine the two vectors you are multiplying ("crossing") as "legs" forming a base for the cross product to "stand on". The more stable the base, the bigger the cross product can be. For example, if you make the legs longer, the base gets bigger and therefore more stable. If the legs are splayed out in opposite directions or squished really close together, though, the base is less stable than if they are perpendicular to each other. In fact, if they're precisely in opposite directions, or precisely in the same direction, there's no base to speak of, so no cross product can stand on them at all. The cross product of two parallel vectors is the null vector. This is also true if either one of the vectors is the null vector.
There's one last thing you need to be aware of. Here we unfortunately have to break with the vectors-are-just-like-numbers theme, because the cross product is anticommutative. This means if you flip the order of a and b in the picture above, you'll get a vector that's still of length |a × b|, but it will be pointing down, not up. This is important:
<math>\vec{a} \times \vec{b} = -(\vec{b} \times \vec{a})</math>
Just like in elementary school you got used to not being able to flip the terms on either side of a subtraction sign at will, you should train yourself not to instinctively flip the ordering of the terms on either side of a cross product sign (unless you are careful to add an extra minus sign or .neg()).
How do you figure out which direction the cross product points? You use the right-hand rule. I find it's confusing to do anything with your index and middle fingers and instead rely on the direction of all my fingers bending at once, but this is something that takes a little bit of experimentation, and works differently for everybody, so twist your right hand (make sure it's your right!) into a bunch of different shapes to see which one best helps you memorize that picture up there. You can also try one of these: http://xkcd.com/199/
What happened to my units?
If you are particularly keen on dimensional analysis, you might be a bit distressed to see that the length of the cross product is equal to the area of a parallelogram. How can an area equal a length? Aren't the two unit systems incompatible?
To resolve this conflict, I have to backpedal a little bit. The name "length" is a misnomer. Nowhere up above did I say that any of these vectors are measured in feet, or meters, or any other "unit of length". In fact, if you are that much of a stickler for dimensional analysis, you've probably taken enough physics that you're used to using vectors for velocities. A velocity isn't measured in units of length either. A more accurate term for this "length" of a vector that I've casually tossed around above is magnitude. This is a unit-agnostic term—I've adopted "length" because this is the term that Emerson uses.
We can restore your dimensional sanity thus: when you multiply two vectors, the units of the result are the units of the first times the units of the second. This is true of both the dot product and the cross product, with the added oddity that the cross product also has a direction in addition to these new, combined units. If the idea of an area having a direction seems weird to you, you can relax: directed areas don't come up too often in game programming. Velocities, momenta, forces, and torques (distance cross force), however, are very common, so don't bind yourself too tightly to the idea of a vector being a distance across space.