Difference between revisions of "User:Wmonroe4/Vectors and Quaternions"
(Created first half of a guide to vectors) |
(Added section on addition and subtraction, plus formatting tweaks) |
||
| Line 1: | Line 1: | ||
I love vectors. | I love vectors. | ||
| − | This is not a typical feeling. Most people find them either scary or completely pointless, or a combination of the two. The problem is that most people are introduced to vectors through 11th-grade pre-calculus, where their teacher shows them that there's something called a "dot product" and a "cross product, | + | This is not a typical feeling. Most people find them either scary or completely pointless, or a combination of the two. The problem is that most people are introduced to vectors through 11th-grade pre-calculus, where their teacher shows them that there's something called a "dot product" and a "cross product", makes them do a few calculations, then moves on to limits or whatever else you do in pre-calculus. (Don't worry, I've forgotten too.) |
The next place you see them, if you've gone this far in math, is Math 51, where they are mostly a notational shorthand for the solution to mind-numbing systems of linear equations, to be solved by Gaussian elimination. Gaussian elimination, if you haven't had to do it, is almost entirely arithmetic, aside from the fact that everything is stuffed into matrices. These arithmetic calculations can be done by a computer. They ''should'' be done by a computer. That is their rightful place. | The next place you see them, if you've gone this far in math, is Math 51, where they are mostly a notational shorthand for the solution to mind-numbing systems of linear equations, to be solved by Gaussian elimination. Gaussian elimination, if you haven't had to do it, is almost entirely arithmetic, aside from the fact that everything is stuffed into matrices. These arithmetic calculations can be done by a computer. They ''should'' be done by a computer. That is their rightful place. | ||
| Line 7: | Line 7: | ||
This is why I was lucky to be exposed to vectors first through 3-D video game development, manipulating them by computer even before I saw them in high school. I learned about vectors by doing things with them, seeing what they ''mean'', as opposed to what is going on with the numbers, which, frankly, does not matter in the slightest. | This is why I was lucky to be exposed to vectors first through 3-D video game development, manipulating them by computer even before I saw them in high school. I learned about vectors by doing things with them, seeing what they ''mean'', as opposed to what is going on with the numbers, which, frankly, does not matter in the slightest. | ||
| − | My hope is that working on Meru will help give you the same love for vectors that I have. The goal of this page to help you take the first step in that direction, and that first step is realizing that vectors are incredibly useful, once you no longer have to do the calculations by hand. So without further verbose introduction, I present: '''How to Put Vectors and Quaternions to Good Use: A guide for game programmers''' | + | My hope is that working on Meru will help give you the same love for vectors that I have. The goal of this page to help you take the first step in that direction, and that first step is realizing that vectors are incredibly useful, once you no longer have to do the calculations by hand. So without further verbose introduction, I present: |
| + | |||
| + | '''How to Put Vectors and Quaternions to Good Use: A guide for game programmers''' | ||
==What's a vector?== | ==What's a vector?== | ||
| Line 33: | Line 35: | ||
<source lang="javascript">>>> v.length() | <source lang="javascript">>>> v.length() | ||
5.385164807134504 | 5.385164807134504 | ||
| − | >>> v.lengthSquared() | + | >>> v.lengthSquared() |
29</source> | 29</source> | ||
| Line 42: | Line 44: | ||
<source lang="javascript">>>> v.normal() | <source lang="javascript">>>> v.normal() | ||
{ | { | ||
| − | x: 0.7427813527082074, // Emerson is printing vectors as y, z, x at the moment | + | x: 0.7427813527082074, // Emerson is printing vectors as y, z, x at the moment. |
| − | y: 0.3713906763541037, // | + | y: 0.3713906763541037, // This film edited for content and formatted to fit your screen. |
z: -0.5570860145311556 | z: -0.5570860145311556 | ||
}</source> | }</source> | ||
| − | Notice that this is in the same ''direction'' as (4, 2, -3), our original: it's a large-ish amount in the ''x'' direction, a slightly smaller amount in the ''y'' direction, and a moderate amount in the negative ''z'' direction. You can do the math, though, or just trust the computer: this new vector has length 1. "Chopping" a vector down to length 1 like this is called '''normalizing''' the vector. | + | Notice that this is in the same ''direction'' as (4, 2, -3), our original: it's a large-ish amount in the ''x'' direction, a slightly smaller amount in the ''y'' direction, and a moderate amount in the negative ''z'' direction. You can do the math, though, or just trust the computer: this new vector has length 1. "Chopping" a vector down to length 1 like this is called '''normalizing''' the vector. Right now it's not clear why this is useful, but be patient: unit vectors come in handy in a surprising number of situations. |
| + | |||
| + | Normalizing a vector gives you a new vector with the same direction and a different length. There's another function that does this in a more general way, letting you multiply the vector's length by an arbitrary factor. It's called <tt>scale</tt>: | ||
| + | |||
| + | <source lang="javascript">>>> v.scale(3) | ||
| + | { | ||
| + | x: 12, | ||
| + | y: 6, | ||
| + | z: -9 | ||
| + | }</source> | ||
| + | |||
| + | See what happened? You got a vector that was triple the length of the original, again in the same direction. There's also a function <tt>div</tt> that divides everything by the number you give it. In fact, with this, you can write <tt>normal</tt> yourself: it's just | ||
| + | |||
| + | <source lang="javascript">return this.div(this.length());</source> | ||
| + | |||
| + | This is pretty much* all the actual Emerson code does. | ||
| + | |||
| + | You can also pass in zero to <tt>scale</tt>, in which case it will just give you (0, 0, 0), the '''null vector'''. You can even pass in a negative number, which in addition to changing its length, makes it point in the ''opposite direction''. Of course, it's still just multiplying numbers behind the scenes. This is just what happens when you multiply all three components by zero or by a negative number. Finally, there's a special shortcut function for scaling by -1, that is, flipping the vector to the opposite direction without changing its length: | ||
| + | |||
| + | <source lang="javascript">>>> v.neg() | ||
| + | { | ||
| + | y: -2, | ||
| + | x: -4, | ||
| + | z: 3 | ||
| + | }</source> | ||
| + | |||
| + | <small>*There's also a minor edge case for when you try to normalize a vector of length zero, to avoid division by zero. That's all there is to it, though.</small> | ||
| + | |||
| + | ==Adding and subtracting vectors== | ||
| + | |||
| + | Here's where things get interesting. Pretty much all of manipulating 3-D objects is combining vectors in various ways. First of all, you can add and subtract them. There are a few ways to think about vector addition. First, you can imagine sticking the tail of one arrow onto the head of the other, with the sum being a third arrow going from the remaining (non-connected) tail to the remaining head. You can also imagine this as "moving along" one vector, then from there "moving along" the other. The sum is how far, and in what direction, you moved ''total''. | ||
| + | |||
| + | The other way to think of it is this: what ''point'' would one vector represent, ''if the point represented by the other were the origin''? This is a particularly useful interpretation in 3-D graphics, where you can have an origin for an object (say, one of those winged frog things from Spore that we've been working with) and a vector representing a point on that object (say, the frog's left eye), which you would then add to a vector representing where the frog is in the world to get an absolute position for the left eye in terms of the whole world. | ||
| + | |||
| + | Notice how I've been careful to say "one vector" and "the other", without mentioning "a", "b", "the first", or "the second". This is because like normal addition, it doesn't matter in what order you add them. '''Vector addition is commutative.''' | ||
| + | |||
| + | From these images you might be able to guess how subtraction works. Just add the first vector to the ''opposite'' of the second. Probably the most useful way to think about this is, "how do I get from the point represented by the ''second'' to the point represented by the ''first''?" Notice that here the order does matter—vector subtraction is not commutative. Just like normal subtraction, '''vector subtraction is anticommutative.''' That is, <math>\vec{a} - \vec{b} = -(\vec{b} - \vec{a})</math>, or in Emerson: | ||
| + | |||
| + | <source lang="javascript">a.sub(b) /* == */ b.sub(a).neg()</source> | ||
| + | |||
| + | <blockquote> | ||
| + | Why have I commented out the <tt>==</tt>? It turns out == doesn't work for vectors, just like it doesn't work for strings in Java. Unfortunately, there isn't an <tt>equals</tt> for vectors in Emerson. You can use this function, if you really need to do this test: | ||
| + | |||
| + | <source lang="javascript"> | ||
| + | function VecEquals(a, b) | ||
| + | { | ||
| + | return (a.x == b.x && a.y == b.y && a.z == b.z); | ||
| + | } | ||
| + | </source> | ||
| + | |||
| + | In any case, these are floating point numbers, so you want to be careful about comparing them. | ||
| + | </blockquote> | ||
| + | |||
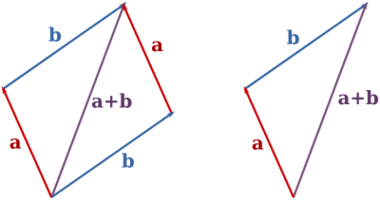
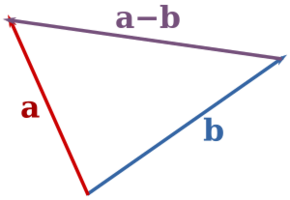
| + | Here's a couple of pictures to help you understand things a bit better: | ||
| − | + | <center> | |
| + | <gallery widths="400" heights="200"> | ||
| + | File:Vector addition.png|Adding two vectors. The triangle picture, I feel, is a better way to think about addition in general; the parallelogram picture is mainly helpful for showing why addition is commutative. (If you can't see the arrowheads, all of the vectors point generally upwards.) | ||
| + | File:Vector subtraction.png|Subtracting one vector from another. The arrowhead of the purple vector points to the left. | ||
| + | </gallery> | ||
| + | </center> | ||
| − | ==Coming soon: products of vectors | + | ==Coming soon: products of vectors, quaternions== |
Revision as of 06:11, 13 April 2011
I love vectors.
This is not a typical feeling. Most people find them either scary or completely pointless, or a combination of the two. The problem is that most people are introduced to vectors through 11th-grade pre-calculus, where their teacher shows them that there's something called a "dot product" and a "cross product", makes them do a few calculations, then moves on to limits or whatever else you do in pre-calculus. (Don't worry, I've forgotten too.)
The next place you see them, if you've gone this far in math, is Math 51, where they are mostly a notational shorthand for the solution to mind-numbing systems of linear equations, to be solved by Gaussian elimination. Gaussian elimination, if you haven't had to do it, is almost entirely arithmetic, aside from the fact that everything is stuffed into matrices. These arithmetic calculations can be done by a computer. They should be done by a computer. That is their rightful place.
This is why I was lucky to be exposed to vectors first through 3-D video game development, manipulating them by computer even before I saw them in high school. I learned about vectors by doing things with them, seeing what they mean, as opposed to what is going on with the numbers, which, frankly, does not matter in the slightest.
My hope is that working on Meru will help give you the same love for vectors that I have. The goal of this page to help you take the first step in that direction, and that first step is realizing that vectors are incredibly useful, once you no longer have to do the calculations by hand. So without further verbose introduction, I present:
How to Put Vectors and Quaternions to Good Use: A guide for game programmers
What's a vector?
It's a bunch of numbers. Or it's a thing with length and direction. These are both definitions of vector, and they're both equally valid. Since the whole point of this page is to mention the ways in which vectors are intuitive and useful, the second definition seems at first glance to be the best one to think about in day-to-day use.
There's an even more useful way to think about a vector, though: a vector is a point. This may seem strange at first. In fact, if you ask a mathematician, she'll tell you that that's just wrong, and strictly speaking, she's right—vectors and points aren't really the same. Treating them as the same thing, however, is an extremely useful practice in 3-D game programming. The most important reason is that it gives you an intuitive link between the collection of numbers and the length-and-direction "arrow" picture. Hopefully high school math has gotten you used to putting points on a Cartesian x-y plane, showing you that a point can be represented by—yes—a bunch of numbers.
But how does a point have length and direction? Well, the point isn't really the whole picture. What that bunch of numbers really tells you is the relationship between that point and some other point. That other point is the origin, some arbitrary spot that we've proclaimed to be the point represented by (0, 0, 0). The fact that we have an origin is what makes points and vectors interchangeable. Now that you have two points, just draw an arrow pointing from the origin to your point, and you've got something with length and direction. Sometimes you won't need to picture the arrow, but if you're lying awake at night wondering whether you are alone in isotropic space, it can be comforting to know that the origin is always there somewhere, throwing invisible arrows out to all your points.
What you can do with one vector
Well, you can take a look at it and examine its properties. Let's make ourselves a vector:
>>> var v = new util.Vec3(4, 2, -3);
>>> v.x
4
>>> v.y
2
>>> v.z
-3
It's clearly got a bunch of numbers. (From here on out you can assume every vector has exactly 3 numbers, unless I specifically say otherwise. A vector doesn't have to be 3-D, but we'll be working mostly with the 3-D kind, so that's what I'll be talking about.) It also has a length:
>>> v.length()
5.385164807134504
>>> v.lengthSquared()
29
lengthSquared isn't always as useful as length, but there's one major advantage to it: it's extremely fast to calculate. Finding the length proper involves taking a square root, which is a lot slower. The best use case for lengthSquared is when you are comparing two lengths: comparing the lengths-squared is faster and works just as well.
What about direction? It's kind of hard to print a direction, but you can do an okay job by coming up with a unit vector—quite simply, a vector of length 1. By arbitrarily saying that a vector must be of length 1, you're saying that you are ignoring its length and focusing only on its direction. This is how you get a normal vector in Emerson:
>>> v.normal()
{
x: 0.7427813527082074, // Emerson is printing vectors as y, z, x at the moment.
y: 0.3713906763541037, // This film edited for content and formatted to fit your screen.
z: -0.5570860145311556
}
Notice that this is in the same direction as (4, 2, -3), our original: it's a large-ish amount in the x direction, a slightly smaller amount in the y direction, and a moderate amount in the negative z direction. You can do the math, though, or just trust the computer: this new vector has length 1. "Chopping" a vector down to length 1 like this is called normalizing the vector. Right now it's not clear why this is useful, but be patient: unit vectors come in handy in a surprising number of situations.
Normalizing a vector gives you a new vector with the same direction and a different length. There's another function that does this in a more general way, letting you multiply the vector's length by an arbitrary factor. It's called scale:
>>> v.scale(3)
{
x: 12,
y: 6,
z: -9
}
See what happened? You got a vector that was triple the length of the original, again in the same direction. There's also a function div that divides everything by the number you give it. In fact, with this, you can write normal yourself: it's just
return this.div(this.length());
This is pretty much* all the actual Emerson code does.
You can also pass in zero to scale, in which case it will just give you (0, 0, 0), the null vector. You can even pass in a negative number, which in addition to changing its length, makes it point in the opposite direction. Of course, it's still just multiplying numbers behind the scenes. This is just what happens when you multiply all three components by zero or by a negative number. Finally, there's a special shortcut function for scaling by -1, that is, flipping the vector to the opposite direction without changing its length:
>>> v.neg()
{
y: -2,
x: -4,
z: 3
}
*There's also a minor edge case for when you try to normalize a vector of length zero, to avoid division by zero. That's all there is to it, though.
Adding and subtracting vectors
Here's where things get interesting. Pretty much all of manipulating 3-D objects is combining vectors in various ways. First of all, you can add and subtract them. There are a few ways to think about vector addition. First, you can imagine sticking the tail of one arrow onto the head of the other, with the sum being a third arrow going from the remaining (non-connected) tail to the remaining head. You can also imagine this as "moving along" one vector, then from there "moving along" the other. The sum is how far, and in what direction, you moved total.
The other way to think of it is this: what point would one vector represent, if the point represented by the other were the origin? This is a particularly useful interpretation in 3-D graphics, where you can have an origin for an object (say, one of those winged frog things from Spore that we've been working with) and a vector representing a point on that object (say, the frog's left eye), which you would then add to a vector representing where the frog is in the world to get an absolute position for the left eye in terms of the whole world.
Notice how I've been careful to say "one vector" and "the other", without mentioning "a", "b", "the first", or "the second". This is because like normal addition, it doesn't matter in what order you add them. Vector addition is commutative.
From these images you might be able to guess how subtraction works. Just add the first vector to the opposite of the second. Probably the most useful way to think about this is, "how do I get from the point represented by the second to the point represented by the first?" Notice that here the order does matter—vector subtraction is not commutative. Just like normal subtraction, vector subtraction is anticommutative. That is, <math>\vec{a} - \vec{b} = -(\vec{b} - \vec{a})</math>, or in Emerson:
a.sub(b) /* == */ b.sub(a).neg()
Why have I commented out the ==? It turns out == doesn't work for vectors, just like it doesn't work for strings in Java. Unfortunately, there isn't an equals for vectors in Emerson. You can use this function, if you really need to do this test:
function VecEquals(a, b) { return (a.x == b.x && a.y == b.y && a.z == b.z); }In any case, these are floating point numbers, so you want to be careful about comparing them.
Here's a couple of pictures to help you understand things a bit better: